Od zákazníků často slýcháváme, že „blackbox“ řešení jsou pro ně neakceptovatelná. V předchozím článku jsme probrali 3 klíčové otázky, které by si měl člověk položit, než takový blackbox model použije. Co ale dělat, pokud jeho úloha není takovému řešení šitá na míru? Použít Bayesovské sítě.
V tomto článku se ponoříme do světa Bayesovských sítí. Začneme základy bayesovského uvažování, které si vysvětlíme na názorném příkladu. Dále si ukážeme, jak pomocí těchto základních kamenů postavit tzv. naivní Bayesův klasifikátor. Od něj je pak už jen krůček ke konstrukci Bayesovské sítě, jak uvidíme v závěru článku.
Krok 1: Jak „bayesovsky“ vyhodnocovat informaci?
Tato část je trochu technická. Ale nebojte se – vše, co budete potřebovat, je středoškolská matematika a jedna rovnice, Bayesův vzorec. Pravděpodobně ho už dávno znáte ze základního kurzu statistiky. My jej zde použijeme ve tvaru pro počítání se šancemi:
Aposteriorní poměr šancí = Apriorní poměr šancí x Poměr věrohodností
Pokud denně nepracujete jako statistik či Data Scientist, mohou vám tato slova znít zvláštně. Jejich význam je ale prostý:
- Apriorní poměr šancí – poměr šancí, že událost nastane, BEZ zohlednění dat. To je to, co si myslíme na začátku.
- Aposteriorní poměr šancí – upravený poměr šancí PO zohlednění dat. To je to, co chceme vědět.
- Poměr věrohodností – technický termín ze statistiky, který vyjadřuje, jakým způsobem ovlivní pozorovaná data naše původní přesvědčení.
A to je všechno. Pojďme si ukázat použití tohoto vzorce na jednoduchém příkladu:
Klient naší banky poslal transakci na neznámý účet a do poznámky napsal „lednice“. Chtěli bychom zjistit, zda šlo o splátkovou transakci, abychom mu případně mohli nabídnout refinancování půjčky.
Karty jsou pak rozdány následovně:
- Otázka: Jaká je šance, že se jedná o splátkovou transakci?
- Pozorování: Poznámka obsahuje slovo „lednice“.
- Apriorní poměr šancí vyjadřuje obecný stav – jak často se vyskytují splátkové transakce? Stanovíme jej jako poměr všech splátkových a všech nesplátkových transakcí, které klienti provedli za sledované období.
- Aposteriorní poměr šancí vyjadřuje naše přesvědčení poté, co zohledníme nález slova „lednice“.
- Poměr věrohodností vyjadřuje sílu „důkazu“. Vypočítáme jej docela snadno: stačí spočítat výskyt slova „lednice“ ve všech splátkových transakcích, pak ve všech nesplátkových transakcích. Nakonec první číslo vydělíme druhým.
Voilà, právě jste použili Bayesův vzorec.
Krok 2: Naivní Bayesův klasifikátor
Transakce s sebou nesou i spoustu dalších atributů jako jsou výše transakce, transakční symboly, opakovanost, pravidelnost aj. Usuzovat pouze z jednoho z nich by proto bylo značně neefektivní. Potřebujeme tedy nějaký způsob, jak tyto střípky informace kombinovat.
Za určitých předpokladů lze postupovat takto:
- Stejně jako výše začneme s apriorním poměrem šancí.
- Pro každý střípek informace, který chceme využít, provedeme následující:
- Použijeme poměr šancí z předchozího kroku jako apriorní poměr šancí v tomto kroku.
- Vyhodnotíme přínos vyšetřované informace pomocí standardního Bayesova vzorce.
- Kýženým výsledkem je aposteriorní poměr šancí po vyhodnocení posledního atributu.
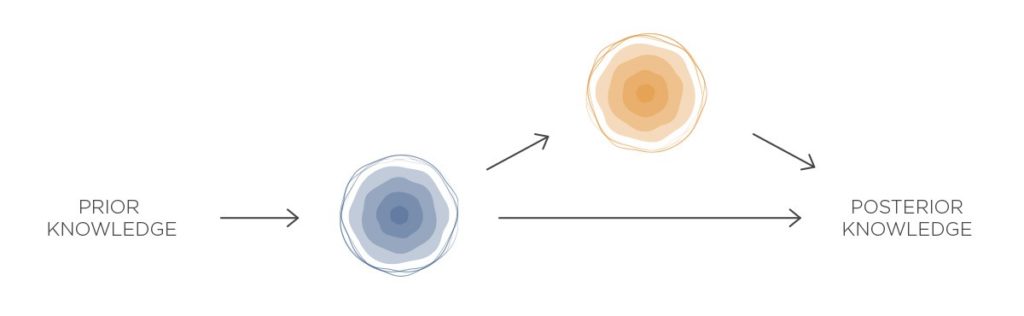
A to je vše. Když si to zakreslíme, připomíná celý proces šňůru korálků:
Tento jednoduchý, ale výkonný model strojového učení se nazývá naivní Bayesův klasifikátor. Jak vidíte, lze jej vypočítat velmi rychle – stačí znásobit několik čísel a máte hotovo. Jednotlivé poměry věrohodností si navíc připravíte dopředu, a tak je ohodnocování transakcí prakticky okamžité.
A jen tak mimochodem – možná jste si toho nevšimli, ale naivní Bayesův klasifikátor používáte denně. Je implementován například ve spam filtru vaší e-mailové schránky. Důkazem, který hledá v příchozích e-mailech, jsou slova zastoupená v nevyžádané poště mnohem častěji než v běžné korespondenci (např. „F r e e“, či „$$$“).
To samozřejmě není jediný případ použití tohoto nástroje. Používá se napříč různými obory – například v medicíně, forenzních vědách (doporučuji k poslechu tuto skvělou přednášku o bayesovském uvažování a forenzní genetice od ScienceCafe.cz), sportovních sázkách apod. Začněme jej tedy používat i v oboru financí a bankovnictví!
Krok 3: Od naivního Bayese k Bayesovským sítím
A teď se trochu vraťme. Před představením naivního Bayesova klasifikátoru jsme zmínili nějaké předpoklady, které musí být splněny. Konkrétně jde o tento požadavek:
- Jednotlivé střípky informace jsou (podmíněně) nezávislé.
To může znít divně. Aniž bychom se pouštěli do matematických detailů, v zásadě musí platit, že:
- Poměry věrohodností použité pro zpřesnění apriorního poměru šancí musí zůstat stejné bez ohledu na již zohledněné střípky informace.
Co to ale znamená v praxi?
- Řekněme, že jsme o transakci zjistili následující dvě věci:
- Výše transakce je vyšší než 100 000 Kč.
- Transakce má v poznámce uvedeno slovo „lednice“.
- Je zřejmé, že tyhle střípky patrně nebudou nezávislé – pokud se jedná o transakci v hodnotě převyšující 100 000 Kč, jen těžko u ní najdeme slovo „lednice“ (jen si takovou ledničku představte!).
- A proto se při znalosti prvního střípku informace změní i poměr věrohodností u střípku druhého.
Výše popsaný způsob tedy použít nemůžeme. Naštěstí zde přicházejí na scénu Bayesovské sítě. Jejich myšlenka je jednoduchá – po vyhodnocení jednoho střípku informace můžeme celý proces rozhodování rozdělit. V našem případě tak druhý důkaz (slovo „lednice“) použijeme jen tehdy, pokud se nejedná o tak vysokou transakci.
Samozřejmě, že musíme poměr věrohodností v tomto oranžovém uzlu odhadnout pouze na odpovídající podmnožině dat (v našem případě na transakcích do 100 000 Kč). Ale logika zůstává stejná, takže to není velký problém.
A voilà, vytvořili jste svou první Bayesovskou síť! Gratulujeme!
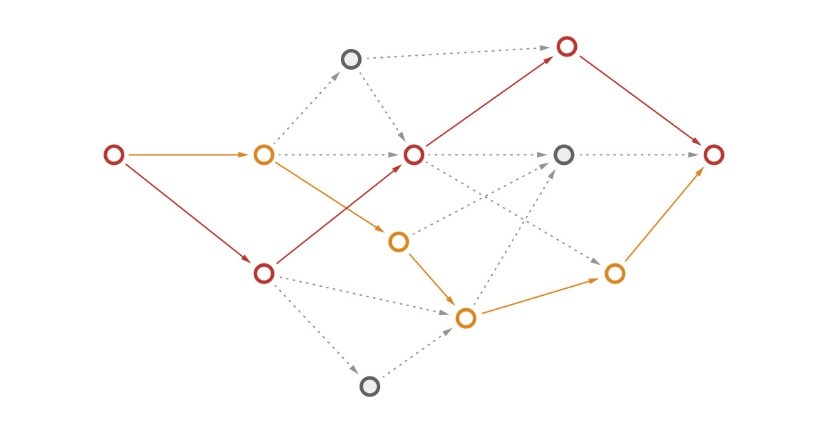
Právě jsme viděli, jak zkombinovat dva střípky informace. Při vyhodnocování nám každý uzel Bayesovské sítě řekne dvě důležité věci – jak upravit svůj dosavadní poměr šancí a jaký důkaz zpracovávat příště. Při kombinaci více uzlů se nám síť snadno rozroste, například takto:
Ale nezapomeňte: základní koncept je stále jednoduchý a jde jen o násobení několika čísel. Ba co víc, takovou Bayesovskou síť si můžete představit jako sadu jednotlivých naivních Bayesových klasifikátorů, jak je naznačeno na obrázku výše. A jejich výstupy, jak už víme, jsou snadno interpretovatelné.
Samozřejmě existuje řada pokročilých způsobů, jak dále zdokonalovat Bayesovské sítě. Můžete vzít v úvahu i další odchozí transakce klienta, můžete přidat více vrstev odrážejících různé úrovně modelování. Časovou složku vám pomohou zohlednit dynamické Bayesovské sítě. A spojité veličiny zase zohlední přístupy tzv. Continuous Bayesian networks.
S výčtem bychom mohli klidně pokračovat. Všechny tyto modifikace jsou velmi zajímavé a některé z nich jsme již implementovali v našich detektorech. Ale popis těchto technik je nad rámec tohoto článku. Máte-li zájem, ozvěte se a můžeme si o nich popovídat osobně.
Autor: Dominik Matula
Data Science Consultant